网络流拓展
本文最后更新于:星期四, 二月 3日 2022, 9:15 晚上
网络流
定义
给定一个有向图,其中每条边都有一个非负的容量值,记做,同时图中存在两个特殊点源点, 汇点。其中从源点到汇点的最大可行流量,这个问题也被称为最大流问题
性质
- 容量限制:对于任意的$ < u, v > \in V,f(u,v)\leq c(u,v)$
- 反对称性:对于任意的$ < u,v > \in V,f(u,v)=-f(v,u)$
- 流量守恒:对于任意的,若不为且不为,那么,即到相邻节点的流量和为,因为流入的流量和流出的流量相等,节点本身不会产生和消耗流量。
解决思路
寻找增广路,不断更新残余网络,直到找不到任何增广路
最大流最小割定理
前言
对于一个网络流,其割的定义是一种点的划分方式,将所有点划分为和两部分,其中源点,汇点。对于一个割,定义净流表示穿过割的流量和。
其中任意一个割的净流总是和网络流的流量相等
解释
根据网络流的定义,只有源点会产生流量,汇点会接收流量。因此对于任意非和的点,净流量一定是,也就是。而源点的流量最终都会经过割的边到达汇点,所以网络流的流等于割的净流
定义
在所有可能的割中,存在一个容量最小的割,我们称其为最小割
对于任意网络流图而言,其最大流一定小于等于最小割
定理
对于一个网络流图,其中有源点和汇点,我们可以推出一个最大流最小割定理
- 流是图的最大流
- 残留网络不存在增广路
- 对于的某一个割,此时
证明
利用反证法,假设是的最大流,但是残留网络中存在增广路,流量为,那么我们又。和矛盾
假设参与网络不存在增广路,所以在参与网络中不存在路径从到达。我们定义集合为:当前残留网络汇中能够到达的点。同时定义
此时构成一个割。且对于任意的有。若则由,可以到达,与属于矛盾
由于的上界是最小割,当到达割的容量的时候,显然达到了最大值,因此是最大流
拓展
二分图多重匹配
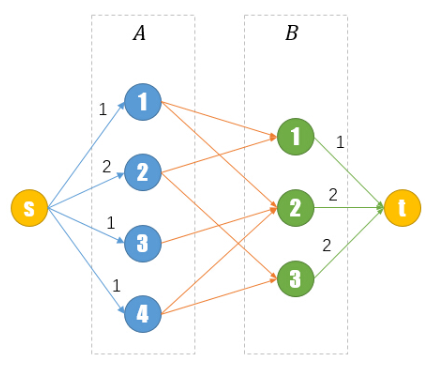
连向,流量为中点可以连接的数量,连向表示可以匹配,连向,流量为可以连接的数量
最小路径覆盖
定义
给定一个有向无环图,用最少的路径数量去保证所有点都被覆盖住
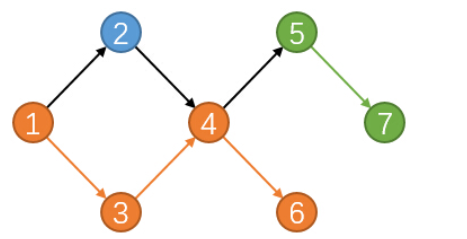
对于每条路径,起点入度都为,终点的出度都为,中间节点的出入读都为
每个点最多有一个前驱,同时最多有一个后继节点
做法
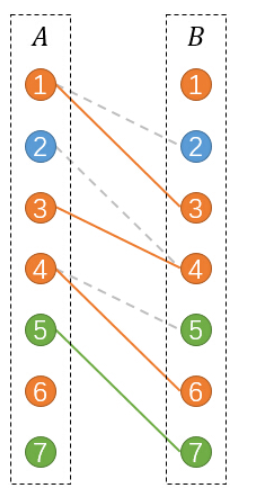
将每个点拆成,其中连向每个,每个连向,对于每条边,建立边,跑网络流,最终答案为点数最大流
最大权闭合子图
定义
给定一有向图,从中选择一些点组成点集。对于每个中的节点,其后续节点仍然需要在中。最权值最大的子图
做法

首先建立源点和汇点,将源点和所有权值为正的点相连,流量为权值,将所有权值为负的点和汇点相连,流量为权值的绝对值,权值为的点不做选择,同时将原来的边的流量设置为无穷大,答案为所有正权值和最小割
引理
- 最小割一定是简单割
- 简单割指得是:割中每一条割边都与或者关联,这样的割叫做简单割。
- 简单割一定和一个闭合子图对应
- 闭合子图和源点构成集,其余点和汇点构成集
证明
-
闭合子图是简单割
-
若闭合子图对应的割不是简单割,则存在一条边,,,且。说明u的后续节点不在中,产生矛盾
-
简单割是闭合子图
-
对于中任意一个点,。的任意一条出边,不会在简单割的割边集中,因此不属于,。所以的所有点均在中,因此是闭合子图
-
最小割就是最大权的闭合子图
-
割的容量中所有正权点的点权之和等于中所有负权点的权值绝对值之和
-
闭合子图的权值中所有正权点的权值之和中所有负权点的权值绝对值之和
-
中所有正权点的权值之和中所有正权点的权值之和所有正权点的权值之和
-
所以所有正权点的权值之和
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!